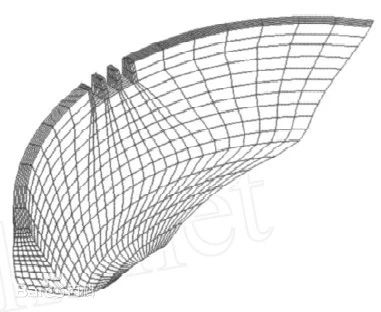
有限元分析（FEA，Finite Element Analysis）利用數學近似的方法對真實物理系統（幾何和載荷工況）進行模擬。利用簡單而又相互作用的元素（即單元），就可以用有限數量的未知量去逼近無限未知量的真實系統。它將求解域看成是由許多稱為有限元的小的互連子域組成，對每一單元假定一個合適的（較簡單的）近似解，然后推導求解這個域總的滿足條件（如結構的平衡條件），從而得到問題的解。因為實際問題被較簡單的問題所代替，所以這個解不是準確解，而是近似解。由于大多數實際問題難以得到準確解，而有限元不僅計算精度高，而且能適應各種復雜形狀，因而成為行之有效的工程分析手段。

有限元分析的基本步驟通常為：

第一步 前處理。根據實際問題定義求解模型，包括以下幾個方面:

(1) 定義問題的幾何區域：根據實際問題近似確定求解域的物理性質和幾何區域。

(2) 定義單元類型:

(3) 定義單元的材料屬性:

(4) 定義單元的幾何屬性，如長度、面積等；

(5) 定義單元的連通性:

(6) 定義單元的基函數;

(7) 定義邊界條件:

(8) 定義載荷。

第二步 總裝求解: 將單元總裝成整個離散域的總矩陣方程(聯合方程組)。總裝是在相鄰單元結點進行。狀態變量及其導數(如果可能)連續性建立在結點處。聯立方程組的求解可用直接法、迭代法。求解結果是單元結點處狀態變量的近似值。

第三步 后處理: 對所求出的解根據有關準則進行分析和評價。后處理使用戶能簡便提取信息，了解計算結果。

縱觀當今國際上CAE軟件的發展情況，可以看出有限元分析方法的一些發展趨勢：

1、與CAD軟件的無縫集成

當今有限元分析軟件的一個發展趨勢是與通用CAD軟件的集成使用，即在用CAD軟件完成部件和零件的造型設計后，能直接將模型傳送到CAE軟件中進行有限元網格劃分并進行分析計算，如果分析的結果不滿足設計要求則重新進行設計和分析，直到滿意為止，從而極大地提高了設計水平和效率。

2、更為強大的網格處理能力

有限元法求解問題的基本過程主要包括：分析對象的離散化、有限元求解、計算結果的后處理三部分。由于結構離散后的網格質量直接影響到求解時間及求解結果的 正確性與否，各軟件開發商都加大了其在網格處理方面的投入，使網格生成的質量和效率都有了很大的提高，但在有些方面卻一直沒有得到改進，因此人們迫切的希望自動六面體網格功能的出現。自適應性網格劃分是指在現有網格基礎上，根據有限元計算結果估計計算誤差、重新劃分網格和再計算的一個循環過程。自適應網格往往是許多工程問題如裂紋擴展、薄板成形等大應變分析的必要 條件。

3、由求解線性問題發展到求解非線性問題

隨著科學技術的發展，線性理論已經遠遠不能滿足設計的要求，許多工程問題如材料的破壞與失效、裂紋擴展等僅靠線性理論根本不能解決，必須進行非線性分析求 解，例如薄板成形就要求同時考慮結構的大位移、大應變（幾何非線性）和塑性（材料非線性）；而對塑料、橡膠、陶瓷、混凝土及巖土等材料進行分析或需要考慮材料的塑性、蠕變效應時，則必須考慮材料的非線性。眾所周知，非線性問題的求解是很復雜的，它不僅涉及到很多專門的數學問題，還必須掌握一定的理論知識和求解技巧，故而學習起來也較為困難。

4、由單一結構場求解發展到耦合場問題的求解

有限元分析方法最早應用于航空航天領域，主要用來求解線性結構問題，實踐證明這是一種非常有效的數值分析方法。而且從理論上也已經證明，只要用于離散求解對象的單元足夠小，所得的解就可足夠逼近于精確值。用于求解結構線性問題的有限元方法和軟件已經比較成熟，發展方向是結構非線性、流體動力學和耦合場問題的求解。例如由于摩擦接觸而產生的熱問題，金屬成形時由于塑性功而產生的熱問題，需要結構場和溫度場的有限元分析結果交叉迭代求解，即"熱力耦合"的問題；當流體在彎管中流動時，流體壓力會使彎管產生變形，而管的變形又反過來影響到流體的流動，這就需要對結構場和流場的有限元分析結果交叉迭代求解， 即所謂"流固耦合"的問題。由于有限元的應用越來越深入，人們關注的問題越來越復雜，耦合場的求解必定成為CAE軟件的發展方向。

5、程序面向用戶的開放性

隨著商業化的提高，各軟件開發商為了擴大自己的市場份額，滿足用戶的需求，在軟件的功能、易用性等方面花費了大量的投資，但由于用戶的要求千差萬別，不管他們怎樣努力也不可能滿足所有用戶的要求，因此必須給用戶一個開放的環境，允許用戶根據自己的實際情況對軟件進行擴充，包括用戶自定義單元特性、用戶自定義材料本構（結構本構、熱本構、流體本構）、用戶自定義流場邊界條件、用戶自定義結構斷裂判據和裂紋擴展規律等等。