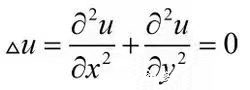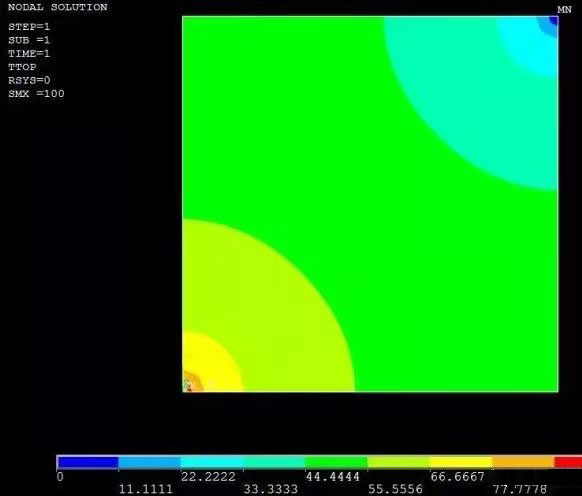
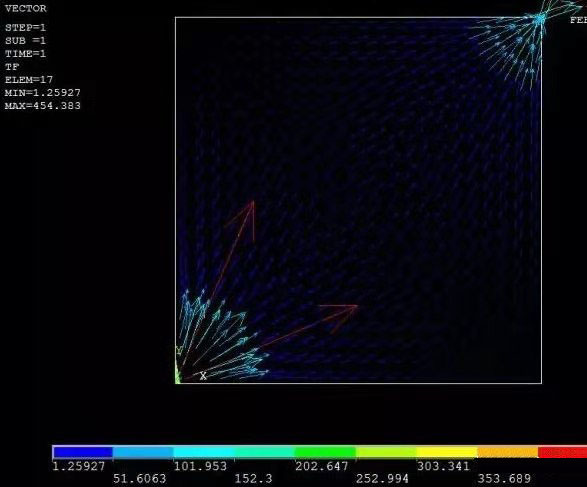
先來看一個平面熱傳導的例子：

該平板左下方的頂點溫度設置100度，右上方頂點設置0度，其它邊自由。

圖1是有限元模型圖，圖2顯示的是溫度場的分布，圖3是溫度梯度向量圖。

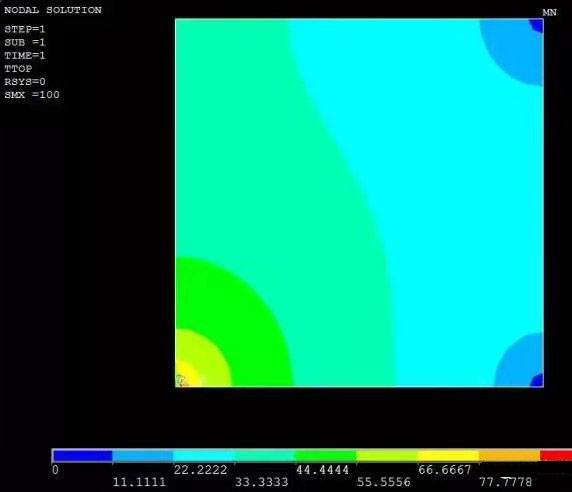
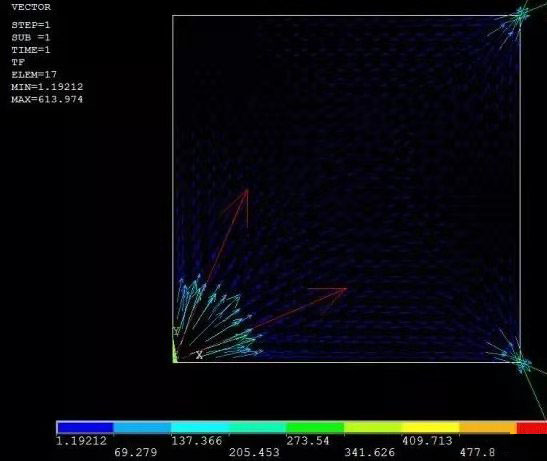
在上面的例子中，右下方的頂點也加上一個溫度為0的約束。

問題來了：

1. 為什么溫度場會服從這種分布，而不是別的形式？

2. 溫度場的分布是否是唯一的？如果是，為什么？

3. 對于這類問題如何求解？

偏微分方程（Partial Differential Equation），簡稱PDE

偏微分方程最早是科學家從振動，熱傳遞等一系列的物理現象歸納總結出來的，實際上絕大部分物理現象都可以用PDE來描述。最常用的PDE都是二階的，即場的導數是二階，高階的PDE也可以通過變換降成二階PDE。

首先介紹導數來預熱， 我們知道 把位移對時間求導，就是速度，把速度對時間再求導就是加速度，簡寫為 a=s(t)'';

a為加速度，S為位移，t為時間；

這個表達式實際上有兩層含義：

1. 位移是時間的函數。例 S(t) = t*t*t-5*t+4， S(t) = sin(t)/cos(2*t);

2. 要使加速度不為0， S(t)一次求導以后必須不為常數，因為常數求導為0。

PDE中要求解的是場函數的表達式，即上面中的S(t)，知道了S(t)的表達式，給出t，就能求出任意時刻的S。

下面是一個典型的二階PDE，其中u為場函數

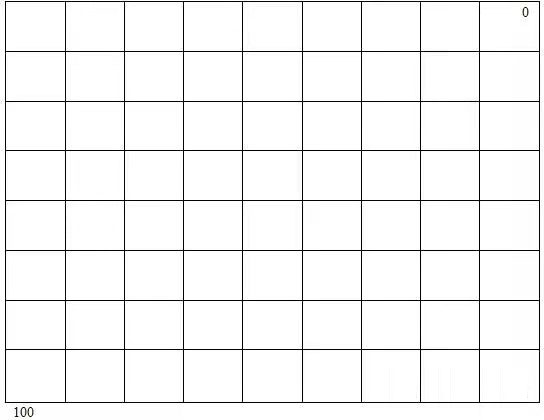
方程看起來很簡單，其實不管是通解，還是定解，u的解析解表達式都是很復雜的，通常都是高階函數，正弦，余弦，指數，對數的組合表達式。理論上PDE都可以找到解析解，但現實大部分PDE的解析解都無法求出。找解析解是數學家們的任務。

該PDE說明u是含有x，y的函數，當對x求導時，y看做常量，對y求導時，x看做常量。

假設 u(x,y)=x*x-y*y+x    ---(1)

u對x求導一次:u'/x=2*x+1; 

u對x求導2次:u''/x=2;

同理對y求導2次:u''/y=-2

說明式1是方程的一個解，但問題是沒有給定邊界條件，方程的解實際上是有無限多個的，要確定定解，必須要設定邊界條件，這也是例子中右下方加上一個新約束，導致溫度場發生變化：即使邊界一個小的變化也可能導致完全不同的定解，即不同的u表達式。

上述方程是無熱源穩態熱傳導的PDE，場函數為溫度，稱為拉普拉斯方程（Laplace，名人得記住），拉普拉斯方程式是電磁，熱，流體，天文等領域經常會碰到的一類數學問題。詳細介紹可參考PDE方面的書。

從上面兩個例子也可以看出，即使很簡單的PDE也是很難找到精確的解析解。找到解析解固然最好，但是找不到也沒關系。就跟圓周率一樣，我們沒必要知道它精確多少位，取7位數對于絕大部分應用足矣。找不到解析解，就只能依靠數值解了，數學家們首先用到的是差分法。

仍然以平面正方形溫度場為例，假設左邊，上，下邊溫度為100度，右邊為0度。 

差分法就是在求解區域畫上 一定密度的結構化網格，如下圖：

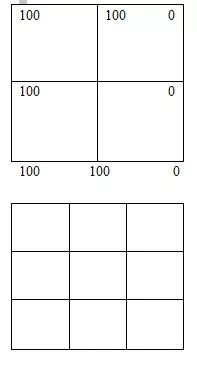
上圖中的任意一個點的溫度值都可以用其周圍臨近的四個點的平均值表示，如果是長方形，表達式會略有不同。將網格簡化如下：

中心點的溫度為 （100+100+100+0）/4 =75 

若將網格加密一些，如上圖，中心四個點為未知量，每個點用周圍四個點的和求平均，可得四個方程，聯立解線性方程組即可，這是差分法的基本思想。

在差分法的基礎上，發展起來的是有限元法。

有限元方法的理論基礎是變分原理和加權余量法。通常有限元方法，變分法，加權余量，以及編程實現之間的關系很容易讓人迷惑。

關于有限元方法的原理，建議直接記住一點：就是伽遼金法(Galerkin)。雖然還有變分，Razi等，但用Galerkin來理解有限元足矣。Galerkin方法是加權余量法的一種。加權余量法的基本原理是：

假設現在有PDE的近似解，而且這個解也滿足邊界條件，那么將這個解帶入PDE，計算結果將產生誤差（因為解場函數是近似的），為了在整個求解區域上保持與精確解相同的特性，就必須想辦法將這些誤差在近似解內部消除掉。

常用加權余量法有：子域法，最小二乘法法，配點法，伽遼金法。使用主要涉及到兩個方面：

1. 如何設計近似解。

理論上可以設計出無限多個近似解，指數，冪數，正弦，余弦等。但是教科書上無一例外的都是以多項式和為主。原因只有一個：簡單。

2. 如何消除誤差。即采用什么方法，強制設置誤差為0，以滿足方程的解。

伽遼金法要求誤差相對于權函數是正交的，即兩者的乘積積分為0。通常權函數為假設的解多項式。將求解區域離散后，不同的單元通過節點連接，節點所連接的每一個單元在該點產生的誤差與設計的權函數乘積積分之后相加為0（有點拗口）.簡單理解就是強制一個節點連接的所有單元在該點產生的誤差和為0。由此可見，一個節點就可以產生一個方程（嚴格來說是一個自由度產生一個方程，因為溫度是標量，一個節點只有一個自由度，如果取位移，平面一個節點就是2個自由度，X和Y兩個方向），最終的解就是節點個數的多項式。

總之任何形式的PDE，離散成網格之后，都可以通過伽遼金方法得到一組近似的線性方程組K*x=F。而且利用伽遼金方法最大的好處就是K是對稱矩陣，方便計算求解。這也是采用伽遼金方法建立有限元方程的主要原因。

說到這里，利用有限元求解PDE原理很簡單：設計近似解，產線性方程組，求解方程組。產生線性方程組的方法有很多，最常用的就是伽遼金法。當微分方程存在相應的泛函時，伽遼金法和泛函可以推導出相同的結果。

如果說差分法和有限元法有什么區別的話，從網格角度看：差分法是把網格畫好然后鋪在求解對象上，而有限元法是直接把對象劃分網格。因此差分法適合求解區域比較規則的幾何，而有限元可以對任意形狀幾何求解。

除伽遼金法外，流體中常用有限體積法，有限體積法采用加權余量法中的子域法。

現在實際上已經回答了前面提出的三個問題：

1. 為什么溫度會服從這種分布，而不是別的形式的？---服從PDE

2. 溫度場的分布是否是唯一的？如果是，為什么？ ---唯一的邊界條件對應唯一的分布

3. 對于這類問題如何求解？---差分法，有限元法，有限體積法

想用通俗的語言來描述有限元，發現其實很難，因為很多東西是需要公式的，有限元本來就是利用積分，微分來解決問題，脫離這些東西講FEM只能算是科普了。